5.面试官：HashMap怎么解决哈希冲突？

大家好，我是牛哥。​

上周跟一个做后端的老兄弟吃饭，他吐槽说前几天面试栽大了 —— 面试官盯着 HashMap 不放，追问‘Hash冲突到底怎么解决？除了链表还有别的方式吗？JDK 1.8 里处理冲突的逻辑跟之前比有啥不一样？’他当时脑子一蒙，只记得链表俩字，后面的红黑树转换、哈希函数优化全想不起来，最后只能灰溜溜地结束面试。​

其实很多同学都一样，平时用 HashMap 存数据挺顺手，可一说到Hash冲突这种底层问题，就容易卡壳，偏偏这种底层问题又是面试的核心考点。

所以今天牛哥就专门跟大家掰扯掰扯，HashMap 到底是怎么解决 Hash 冲突的，我们会从解决冲突的思路，讲到底层源码的设计、相关方案的对比，不管是正在准备面试的同学，还是想补底层知识的开发者，今天这篇文章都能帮你把哈希冲突的 “根” 和 “解法” 捋明白，下次再被问，就能说得又准又透彻。​

解决Hash冲突的思路

什么是哈希冲突？简单来说，就是两个不同的键（比如用户 ID、订单号），经过哈希函数计算后，得到了相同的哈希值，最终指向 HashMap 里同一个桶，这就叫哈希冲突。

HashMap 解决哈希冲突的逻辑可以从 预防 和 解决 两个层面来看，整个过程和它的底层结构紧密相关。

首先，HashMap 底层是数组（哈希表）加链表 / 红黑树的组合结构。当我们存放键值对时，会先通过 key 的 hashCode 计算哈希值，再经过扰动函数（多次异或和右移）处理，让哈希值的高位也参与运算，最后对数组长度取模得到索引位置。这个过程本身就是在减少冲突 —— 扰动函数能让哈希值分布更均匀，降低不同 key 计算出相同索引的概率。

如果还是出现了冲突，即不同 key 落到同一数组索引，大的方向有两个：拉链法和开放地址法，下面我们就详细聊聊这两个方向。

直面冲突：拉链法

拉链法，又称链地址法，其思路很直接：哈希表底层是数组，当不同元素计算出相同索引时，就在该数组位置挂一个链表，把所有冲突元素都存到这个链表中。查询时，先定位到数组索引，再遍历链表找到对应元素。

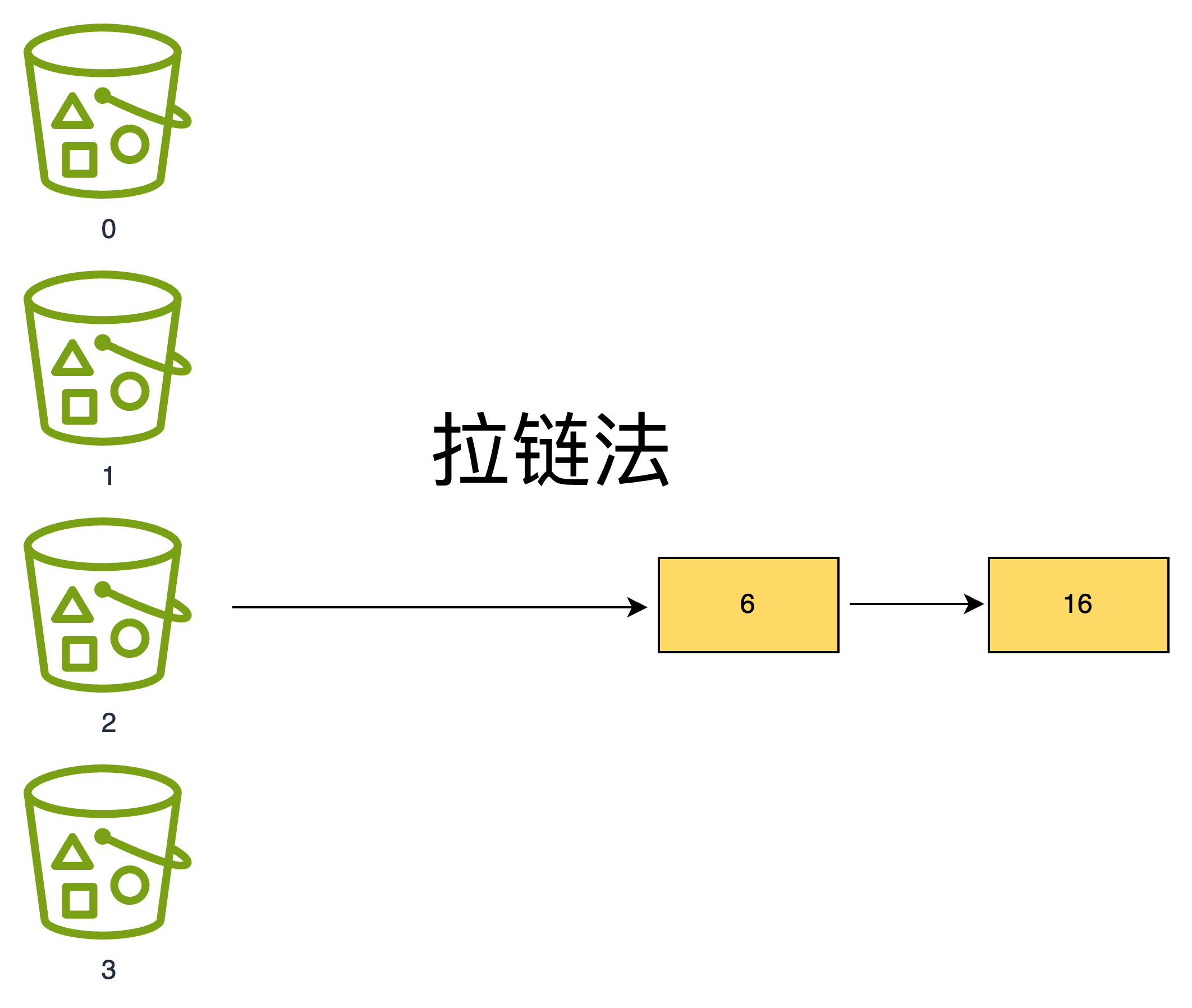
移形换位：开放地址法

开放地址法则是另一种思路：发生冲突时，不额外创建链表，而是在哈希表内部重新寻找空闲位置存储元素。

比如线性探测法，若索引 i 冲突，就检查 i+1、i+2…… 直到找到空位。这种方法不需要额外指针空间，内存利用率高，但容易出现 “聚集现象”—— 连续的空位被占用后，新元素需要探测更远的位置，导致效率下降，而且删除元素时不能直接清空位置，因为可能破坏探测链，需要做标记处理，没有拉链法直观。

Java的HashMap用的哪一种方法

Java 中的 HashMap 就是拉链法典型例子，Java 7 中，HashMap 解决哈希冲突仅依赖「数组 + 单向链表」结构，冲突元素通过头插法加入链表。

// Java 7 中 HashMap 的 put 方法核心逻辑
public V put(K key, V value) {
    if (table == EMPTY_TABLE) {
        inflateTable(threshold); // 初始化数组
    }
    if (key == null)
        return putForNullKey(value); // 处理 null key
    
    int hash = hash(key); // 计算哈希值
    int i = indexFor(hash, table.length); // 计算数组索引
    
    // 遍历链表，查找是否有相同 key
    for (Entry<K,V> e = table[i]; e != null; e = e.next) {
        Object k;
        // 哈希值相同且 key 相等，覆盖 value
        if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
            V oldValue = e.value;
            e.value = value;
            e.recordAccess(this);
            return oldValue;
        }
    }
    
    modCount++;
    // 没有相同 key，新增节点（头插法）
    addEntry(hash, key, value, i);
    return null;
}

不过在Java 7中，因为使用头插法处理哈希冲突，当多线程并发扩容时可能产生环形链表，根源在于头插法的链表反转机制与并发操作的冲突。

// 新增节点到链表（头插法）
void addEntry(int hash, K key, V value, int bucketIndex) {
    // 检查是否需要扩容
    if ((size >= threshold) && (null != table[bucketIndex])) {
        resize(2 * table.length); // 扩容为原来的 2 倍
        hash = (null != key) ? hash(key) : 0;
        bucketIndex = indexFor(hash, table.length);
    }
    // 创建新节点，插入到链表头部
    createEntry(hash, key, value, bucketIndex);
}

void createEntry(int hash, K key, V value, int bucketIndex) {
    Entry<K,V> e = table[bucketIndex];
    // 新节点的 next 指向原链表头部，实现头插
    table[bucketIndex] = new Entry<>(hash, key, value, e);
    size++;
}

具体来说，HashMap 扩容时会创建新数组，并将旧数组中的链表迁移到新数组。头插法会将旧链表的节点按逆序插入新链表（即新节点总是放在链表头部）。当多个线程同时对同一个链表进行迁移时，可能出现线程 A 已处理部分节点，线程 B 又对同一批节点进行操作的情况。

例如，线程 A 已将节点 1→节点 2 的链表迁移为节点 2→节点 1，而线程 B 此时可能仍持有旧的节点引用，继续处理时会错误地将节点 1 的 next 指向节点 2，同时节点 2 的 next 又指向节点 1，形成环形链表。后续环形链表会导致后续 get 操作时陷入无限循环，引发程序卡死。

Java 8 引入了红黑树 优化长链表性能，同时改用尾插法，不用再翻转顺序，解决了链表环问题。

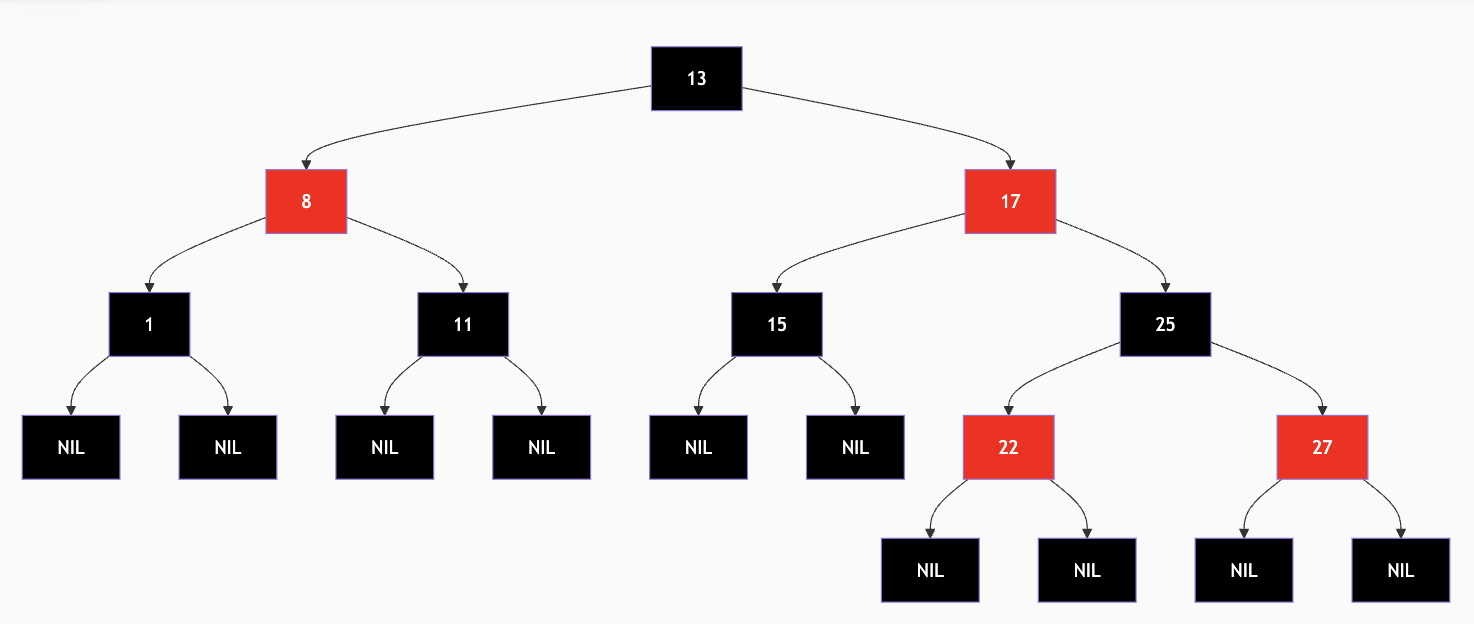
可以结合如下代码理解：

// Java 8 中 HashMap 的 put 方法核心逻辑
public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length; // 初始化或扩容
    
    // 计算索引，如果该位置为空，直接放新节点
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
    else {
        Node<K,V> e; K k;
        // 相同 key，覆盖 value
        if (p.hash == hash && 
            ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;
        // 该位置是红黑树节点，按树结构插入
        else if (p instanceof TreeNode)
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        // 该位置是链表，遍历链表
        else {
            for (int binCount = 0; ; ++binCount) {
                if ((e = p.next) == null) {
                    // 尾插法：新节点放在链表尾部
                    p.next = newNode(hash, key, value, null);
                    // 链表长度超过 8，转为红黑树
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        treeifyBin(tab, hash);
                    break;
                }
                // 找到相同 key，退出循环
                if (e.hash == hash && 
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }
        if (e != null) { // existing mapping for key
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e);
            return oldValue;
        }
    }
    ++modCount;
    // 检查是否需要扩容
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    return null;
}

链表转红黑树的具体逻辑如下：

// 链表转红黑树
final void treeifyBin(Node<K,V>[] tab, int hash) {
    int n, index; Node<K,V> e;
    // 数组长度小于 64 时先扩容，不转树
    if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
        resize();
    else if ((e = tab[index = (n - 1) & hash]) != null) {
        TreeNode<K,V> hd = null, tl = null;
        do {
            TreeNode<K,V> p = replacementTreeNode(e, null);
            if (tl == null)
                hd = p;
            else {
                p.prev = tl;
                tl.next = p;
            }
            tl = p;
        } while ((e = e.next) != null);
        if ((tab[index] = hd) != null)
            hd.treeify(tab); // 转为红黑树
    }
}

这块逻辑看似复杂，但它的核心思路其实很简单，就是链表太长会导致查询效率下降，时间复杂度接近 O (n)，所以当链表长度超过 8，且数组长度大于 64 时，会把链表转为红黑树，此时查询、插入的效率能提升到 O (log n)。

如果数组长度不足 64，会先触发扩容而不是树化，因为小容量数组扩容后冲突概率会自然降低。

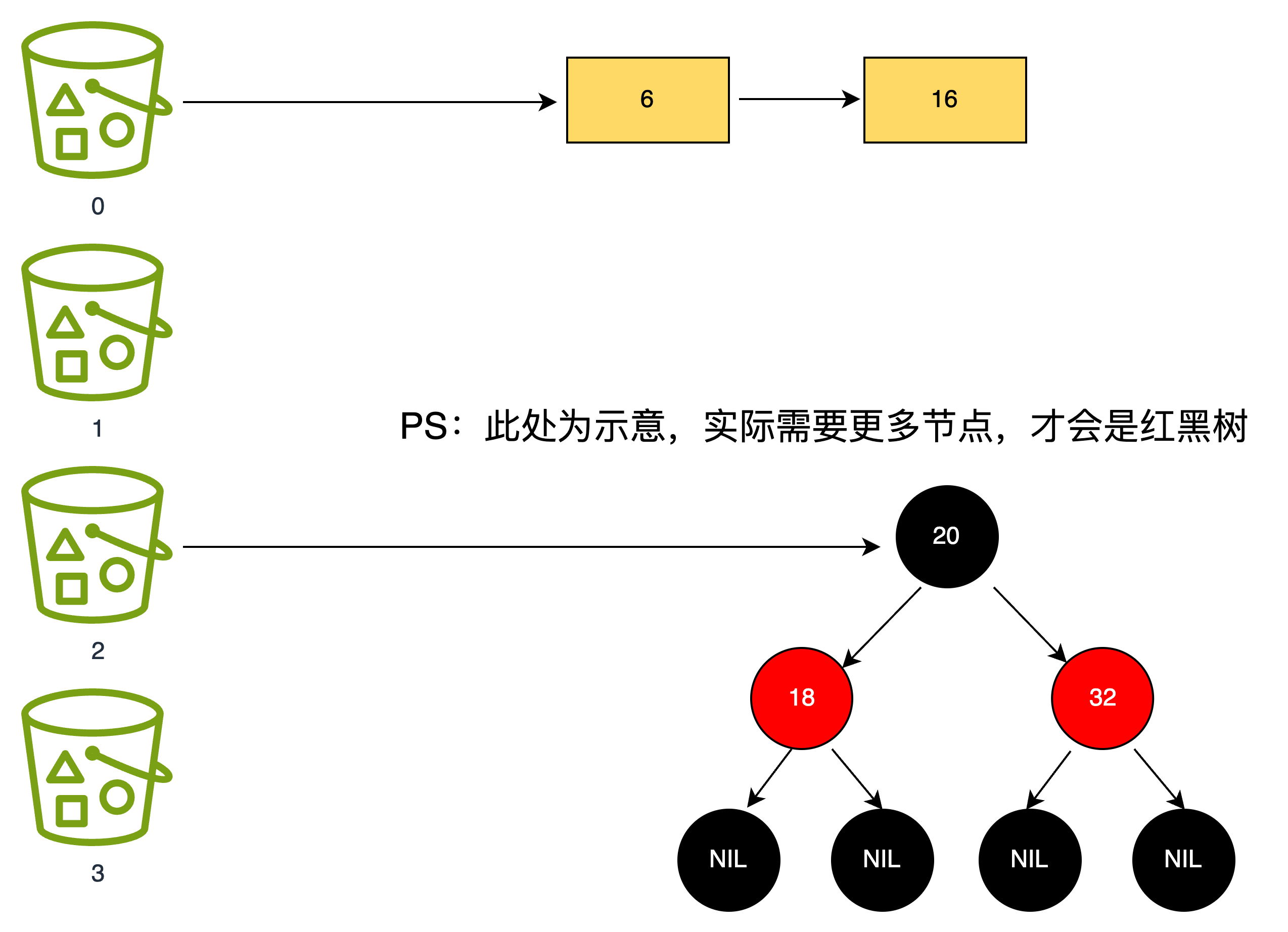
HashMap具体是怎么扩容的？

HashMap 扩容是为了解决容量不足引起的哈希冲突。其扩容触发主要有两个条件：

一个是整体元素数量超过 threshold = capacity × loadFactor（默认为 16×0.75=12）。

loadFactor就是负载因子，是衡量 HashMap 空间使用效率的关键参数。负载因子值越大，数组使用越充分，但冲突概率上升，链表/树结构加长，降低查询效率。反之，负载因子越小，查找快但浪费空间。

JDK 选择 0.75 这一经验值，是经过大量性能测试得出的权衡结果——在实际业务中能达到较好的查找效率，又不会因频繁扩容而增加性能开销。若有特殊场景，可通过构造函数手动设置更适配的负载因子。

另一个是在 Java 8 中，如果单个桶内链表长度达到 8 且当前数组长度小于 64，也会触发扩容而非转红黑树。

扩容时，HashMap 会将原数组中的元素重新计算 hash 后搬迁到新数组，扩容代价较大，因此应尽量通过构造函数提前指定合适初始容量，减少 resize 次数，提升性能。

HashMap 的默认初始容量为什么是 16？

HashMap 的默认容量为 16（2^4），这一数值不是随意选择的，而是根据实际应用中的负载均衡与性能表现做出的折中。容量过小，比如4或8，在面对较多元素时容易频繁扩容，影响性能；

过大则会导致内存浪费，16 是一个恰当的起点：结合默认负载因子 0.75，首次扩容会在存入 12 个元素后触发，既保障性能，又利于控制空间开销。此外，16 是 2 的幂次，便于 hash 计算。JDK 虽未在文档中显式说明原因，但这是一种基于历史实践的合理经验值。

扩容之后的位置怎么计算的

这个问题，1.8版优化之后，其实有点晦涩。

我们用生活场景 + 二进制计算结合的方式，彻底讲透这个优化点。先记住一个核心前提：HashMap 的数组长度永远是 2 的幂（如 16、32、64...），扩容时直接翻倍。

场景类比：给学生排座位，假设学校的教室座位是 “2 的幂” 排列：

初始有 16 个座位（编号 0-15），学生按 “学号的后 4 位” 找座位（比如学号后 4 位是 0101，坐 5 号）。

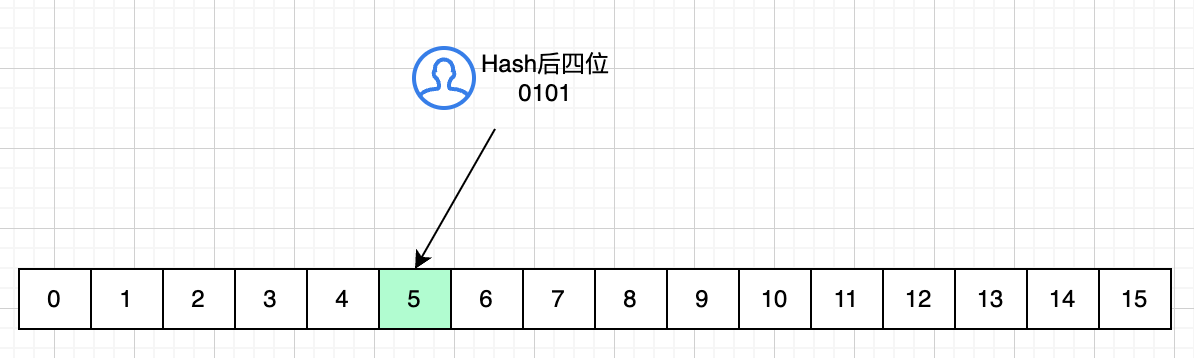
后来学生变多，座位扩容到 32 个（编号 0-31），此时需要重新排座位，Java 7 和 Java 8 的区别，就像两种不同的排座位方式。

Java 7 的排法：重新算学号再找座位

原来 16 个座位时，按 “学号后 4 位” 排（如学号xxxx0101→5 号）。

扩容到 32 个座位后，Java 7 要求重新计算学号（比如把原学号打乱重算），再按 “新学号的后 5 位” 排座位（如yyyy10101→21 号）。

这里的 “重新计算学号” 就是 Java 7 的问题：明明只是座位变多了，却要重复计算哈希值（类似重算学号），完全没必要。

Java 8 的排法：只看 “新增的一位”

Java 8 发现，座位从 16→32，本质是座位编号从 “4 位二进制”（0000-1111）变成 “5 位二进制”（00000-11111）。新增的第 5 位（最高位）决定了新座位的位置。

用二进制具体计算：

原座位（16 个）：位置 = 哈希值 & 15（15 是 16-1，二进制1111），本质是取哈希值的低 4 位（如哈希值低 4 位0101→5 号）。

扩容后（32 个座位）：新位置 = 哈希值 & 31（31 是 32-1，二进制11111），本质是取哈希值的低 5 位。

对比原位置和新位置的低 5 位：

前 4 位和原位置的低 4 位完全相同（比如原低 4 位0101，新低 5 位可能是00101或10101）。

唯一的区别是新增的第 5 位（从右数第 5 位）：

若第 5 位是0 → 新位置 = 原位置（如00101→5 号）。

若第 5 位是1 → 新位置 = 原位置 + 16（旧长度，也就是多的那个1）（如10101→5+16=21 号）。

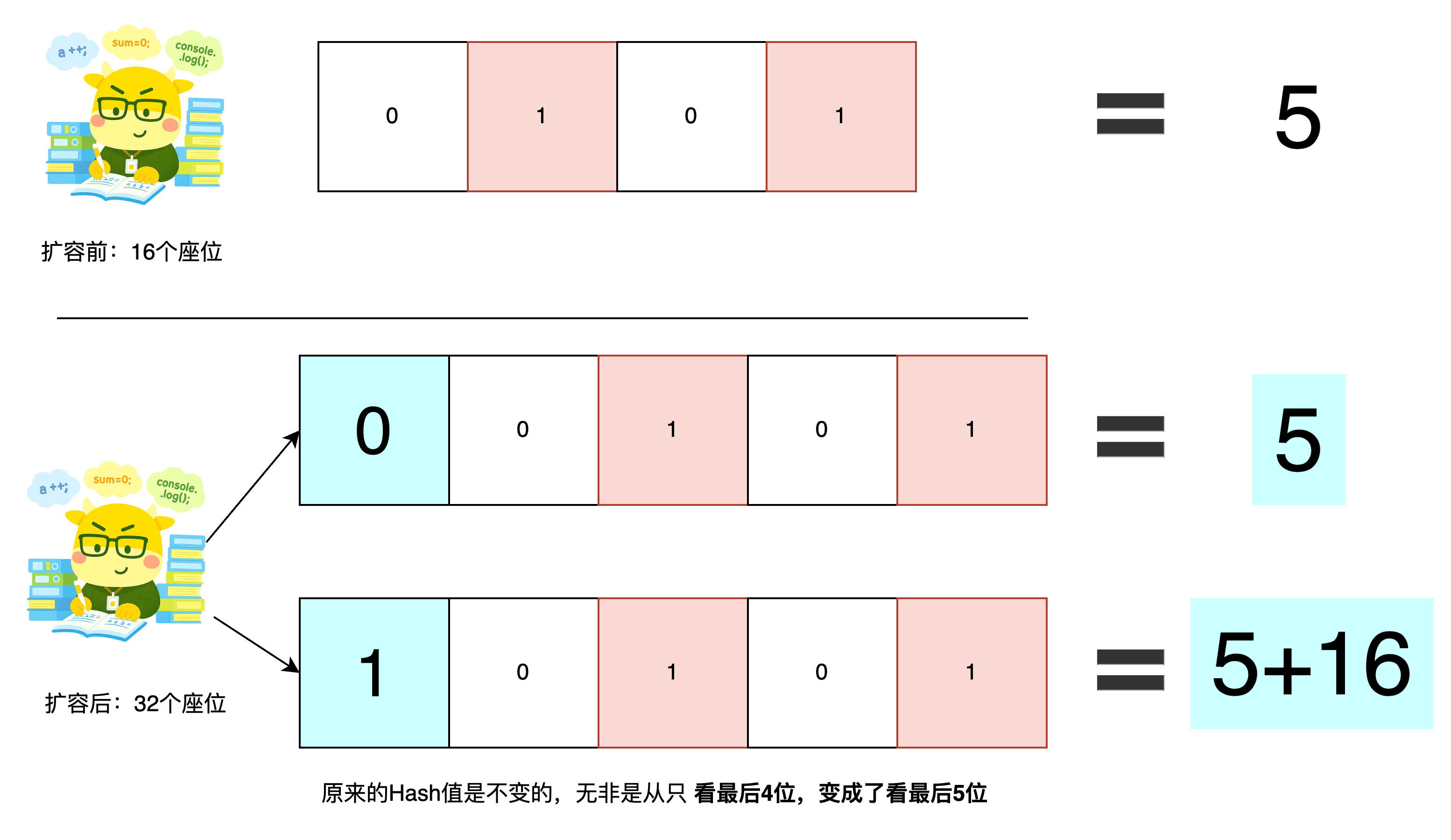
为什么这样更高效

原哈希值已经包含了所有信息，没必要重新计算（就像学号没变，只是座位变多了，不用重算学号）。

只需判断哈希值中 “旧长度对应的那一位”（16 对应的是第 4 位，32 对应的是第 5 位），1 次判断就能确定新位置，比 Java 7 的 “重算哈希 + 重新计算位置” 快得多。

Java 8 的优化本质是：利用 “数组长度翻倍” 的特性，通过哈希值中 “新增的一位” 直接确定新位置，避免重复计算哈希。就像从 “4 位数座位号” 变 “5 位数” 时，只需看第 5 位是 0 还是 1，就能快速找到新座位，既简单又高效。

HashMap链表转红黑树的阈值是怎么定的？

前面我们有提到，当链表长度超过 8，且数组长度大于 64 时，会把链表转为红黑树，那你有没有想过这个阈值8是怎么来的？

这一阈值并非随意设定，而是基于泊松分布等实证数据得出的结论：哈希碰撞超过 8 次的概率非常小，若真的发生了，说明哈希算法或 key 分布存在问题，此时使用红黑树可显著提升查找性能。

那你再猜一下什么时候红黑树转回链表吗？答案是反直觉的：当数组长度小于64，且链表长度小于6时，才会反转回红黑树。这个设计是为了避免在节点数反复波动于 7 附近时频繁切换树与链表。

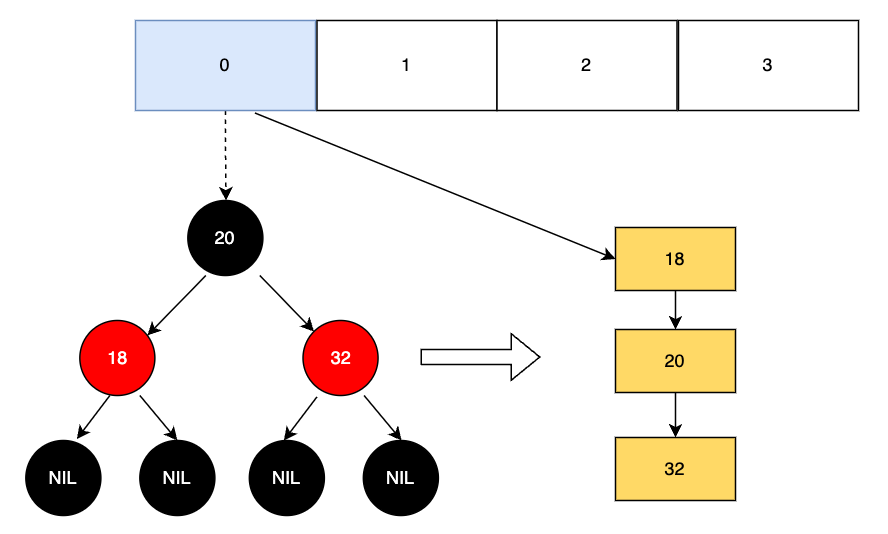
Java 8 为什么使用红黑树而不是 AVL 树？

讲到这里，相信你对如何应对Hash冲突已经了如指掌，这里我们再扩展思考一下，Java 8 为什么使用红黑树而不是 AVL 树？

我们先介绍一下什么是AVL树，它的本质是自平衡二叉搜索树，是最早提出的平衡树结构之一，它是由两位苏联科学家 Adelson-Velsky 和 Landis 在 1962 年发明，名字就来自他俩的缩写。

它的核心特点就一个：严格平衡—— 不管怎么增删节点，都能通过调整，保证任意节点的左右子树高度差不超过1。

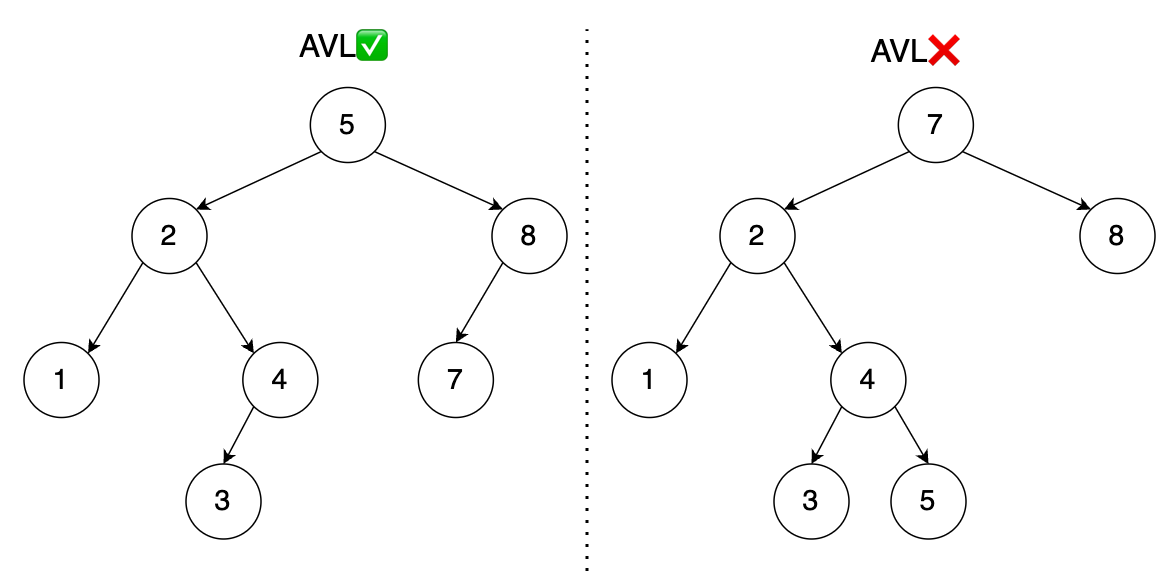
因为严格平衡，AVL 树的高度是最矮的二叉搜索树，比如 n=1000 时，树高最多 10 层，这是它最大的优势，适合查询密集场景。

既然AVL树这么好，为什么Java8选择用红黑树呢？

主要是如下两个原因：

• AVL 树在插入/删除操作后保持严格的高度平衡，虽然查找效率略高于红黑树，但为了保持这种平衡，其插入删除时需频繁做旋转，代价较大。

• 而红黑树在保持大致平衡的基础上，通过颜色标记限制最长路径，结构调整相对简单，插入删除开销小。

在 HashMap 的应用场景中，更多关注的是插入性能与平均查找效率的平衡，极端场景也较少，因此红黑树是更合适的选择。JDK 也广泛采用红黑树作为 TreeMap、TreeSet、ConcurrentSkipListMap 等结构的底层实现。

总结

面试中想答好 HashMap 哈希冲突，先明确核心定义 —— 不同键经哈希函数计算后，指向同一 “桶” 就是冲突；再记清 Java 的三大解决关键：靠扰动函数减少初始冲突，用链表转红黑树避免查询卡顿，借扩容机制缓解冲突压力。​

牛哥也希望各位粉丝朋友，不管是准备面试还是深耕业务，都能把这些底层逻辑吃透，既能在面试里稳稳拿分，写代码时也能少踩坑、效率高，后续不管是跳槽涨薪还是技术深耕，都顺顺利利，一路进阶！